Unidad III. Autómatas Finitos

3.1 Conceptos: Definición y Clasificación de Autómata Finito (AF)

Los autómatas finitos son reconocedores; sólo dicen “sí” o “no” en relación con cada posible cadena de entrada.

Los autómatas finitos pueden ser de dos tipos:

• Los autómatas finitos no deterministas (AFN) no tienen restricciones en cuanto a las etiquetas de sus líneas. Un símbolo puede etiquetar a varias líneas que surgen del mismo estado, y ϵ, la cadena vacía, es una posible etiqueta.

• Los autómatas finitos deterministas (AFD) tienen, para cada estado, y para cada símbolo de su alfabeto de entrada, exactamente una línea con ese símbolo que sale de ese estado.

Tanto los autómatas finitos deterministas como los no deterministas son capaces de reconocer los mismos lenguajes. De hecho, estos lenguajes son exactamente los mismos lenguajes, conocidos como lenguajes regulares, que pueden describir las expresiones regulares.

Autómata Finito No Determinista (AFND) para una expresión regular

Intuitivamente un autómata finito consta de un conjunto de estados y, partiendo de un estado inicial, realiza transiciones de un estado a otro en respuesta a los símbolos de entrada que procesa. Cuando el autómata alcanza un estado de los que se denominan finales, se dice que ha reconocido la palabra formada por concatenación de los símbolos de entrada procesados.
Un autómata finito puede ser determinista o no determinista. La expresión «no determinista» significa que desde un mismo estado puede haber más de una transición etiquetada con el mismo símbolo de entrada.
Un autómata finito no determinista es una quíntupla (Σ, Q, δ, q0, F), donde:

1. Σ es un conjunto finito de símbolos de entrada o alfabeto.
2. Q es un conjunto finito de estados.
3. δ es la función de transición que recibe como argumentos un estado y un símbolo de entrada o el símbolo λ y devuelve un subconjunto de Q.
4. q0 ∈ Q es el estado inicial.
5. F ⊆ Q es el conjunto de estados finales.

Un autómata finito puede representarse mediante lo que se conoce como diagrama de transición, que es un grafo dirigido construido de la siguiente forma

• Cada nodo está etiquetado con un elemento de Q.
• Si δ(p,a) = q, se dibuja un arco del nodo con etiqueta p al nodo con etiqueta q etiquetado con el símbolo a.
• El estado inicial aparece señalado con una flecha sin origen.
• Los estados finales aparecen marcados con un doble círculo.

Figura 1.0 Diagrama de transición para un autómata.

El diagrama de transición para el autómata finito determinista ({0,1},{p,q,r},δ,p,{q}), de la figura 1.0, muestra δ que está definida de la siguiente forma:

δ(p,0)=q	δ(p,1)=r	δ(q,0)=q
δ(q,1)=r	δ(r,0)=r	δ(r,1)=r

Para toda expresión regular e es posible construir un autómata finito no determinista que acepte el lenguaje generado por dicha expresión regular. El algoritmo es recursivo y consta de los siguientes pasos:

  1. Si e = Φ, el autómata correspondiente es el que aparece en la figura 1.1 (a).

  2. Si e = λ, el autómata correspondiente es el que aparece en la figura 1.1  (b).
  3. Si e = a, a ∈Σ, el autómata correspondiente es el que aparece en la figura 1.1 (c).

Figura 1.1 Autómatas para expresiones regulares básicas

  4. Si e=r|sy tenemos los autómatas correspondientes a r y s, que representaremos como aparecen en la figura 1.2, el autómata correspondiente a la expresión r|s es el que aparece en la figura 1.3 (a).

Figura 1.2 Autómatas correspondientes a las expresiones r y s.

  5. Si e = rsy tenemos los autómatas correspondientes a r y s, que representaremos como aparecen en la figura 1.2, el autómata correspondiente a la expresión rs es el que aparece en la figura 1.3 (b).

Figura 1.3 Autómatas correspondientes a las expresiones r|s y rs.

  6. Si e = r*y tenemos el autómata correspondiente a r, que representaremos como aparece en la figura 1.4 (a), el autómata correspondiente a la expresión r* es el que aparece en la figura 1.4 (b).

Figura 1.4 Autómatas correspondientes a las expresiones r y r*.

Autómata Finito Determinista (AFD) equivalente a un AFND

Un autómata finito determinista es una quíntupla (Σ, Q,δ, q0, F), donde

• Σ es un conjunto finito de símbolos de entrada o alfabeto.
• Q es un conjunto finito de estados.
• δ es la función de transición que recibe como argumentos un estado y un símbolo de entrada y devuelve un estado.
• q0 ∈ Q es el estado inicial.
• F ⊆ Q es el conjunto de estados finales.

La función de transición extendida recibe como argumentos un estado p y una cadena de caracteres wy devuelve el estado que alcanza el autómata cuando parte del estado p y procesa la cadena de caracteres w. Dado un autómata finito no determinista N= (Σ, Q, f, q 0, F) siempre es posible construir un autómata finito determinista D= (Σ, Q´, f´, q0´, F´) equivalente (que acepte el mismo lenguaje).

Para construir dicho autómata seguiremos el siguiente procedimiento: 

• Cada estado de D corresponde a un subconjunto de los estados de N. En el autómata de la Figura 1.5 (c):

Figura 1.5 AFND para la expresión regular digito.digito*.

• Los subconjuntos {q1}, {q3, q4} o {q2, q4, q6} serían posibles estados del autómata finito determinista equivalente.
• El estado inicial q0´ de D es el resultado de calcular el cierre λ del estado inicial q0 de N. El cierre λ de un estado e se representa como ē y se define como el conjunto de estados alcanzables desde e mediante cero o más transiciones λ. En el autómata de la Figura 1.5 (c) el cierre λ de cada uno de los estados son las siguientes:

• Desde un estado P de D habrá una transición al estado Q con el símbolo a del alfabeto. Para calcular esta transición calculamos primero un conjunto intermedio P_a formado por los estados q de N tales que para algún p en P existe una transición de p a q con el símbolo a. El estado Q se obtiene calculando el cierre λ del conjunto P_a.

Partiendo del AFND de la Figura 1.5 (c), la transición desde el estado inicial {q1} con el símbolo digito se calcularía de la siguiente forma:

• Puesto que δ(q4,digito)=q5, la transición desde el estado {q2,q3,q4,q6} con el símbolo digito será: 

• Puesto que δ(q4,digito)=q5, la transición desde el estado {q5,q4,q6} con el símbolo digito será:

Figura 1.6 Autómata finito determinista correspondiente al AFND de la Figura 1.5

• En el autómata finito determinista D un estado será final si contiene algún estado final del AFND N. En el AFD correspondiente al autómata de la Figura 1.5 (c), serán estados finales todos aquellos que contengan el estado q6. La Figura 1.6 muestra el AFD equivalente al AFND de la Figura 1.5 (c)..

3.2 Conversión de un Autómata Finito No Determinista (NFA) a Autómata Finito Determinista (DFA)

Dado un NFA M ≡ (Σ, Q, F, q0, d), $ DFA M' º (å', Q', F', q´0, d’) | L(M)=L(M')

• Q'=à(Q)
• å = å'
• q´0={q0} (conjunto de estados que contiene el de arranque del NFA)
• F' Í Q' (aquellos subconjuntos de Q que contengan algún pÎF)
• d '({q1, q2, ... q k}, a) = {p1, p 2 ... pm}Ûd ({q1, q2, ... qk}, a) = {p1, p 2 ... p m}

Para construir un DFA a partir de un NFA, se procede del siguiente modo:

• Se toman todos los símbolos å, y se aplica d sobre el símbolo inicial, q0.
• Al hacer eso, darán como resultado un conjunto A Î  Ã (Q), que añadiremos a una lista de Estados nuevos.
• Se denomina marcar un estado a aplicar la función d sobre todos los símbolos del alfabeto. A partir de ahí hay que marcar todos los estados nuevos que nos salgan.
• El algoritmo para una vez estén marcados todos los estados nuevos serán estados de aceptación aquellos estados que contengan algún estado de aceptación del NFA. Por último se dibuja el diagrama de transiciones

3.3 Representación de ER usando AFND

Ejemplo de ER convertida en AFND

A partir de una ER y de las construcciones de Thomson vamos a obtener el AFND equivalente.

En este caso la ER será: (a|b+)b?.

3.4 Minimización de estados enun AF

Dos estados de un autómata finito determinista son estados equivalentes si al unirse en un sólo estado, pueden reconocer el mismolenguaje regular que si estuviesen separados. Esta unión de estados implica la unión tanto de sus transiciones de entrada como de salida. Si dos estados no son equivalentes, se dice que son estados distinguibles. Un estado final con un estado no-final nunca serán equivalentes.

Un AFD está minimizado, si todos sus estados son distinguibles y alcanzables. Un algoritmo de minimización de AFD es el siguiente:

Eliminar los estados inaccesibles del autómata.

Construir una tabla con todos los pares (p, q) de estados restantes.

Marcar en la tabla aquellas entradas donde un estado es final y el otro es no-final, es decir, aquellos pares de estados que son claramente distinguibles.

Para cada par (p, q) y cada símbolo a del alfabeto, tal que r = δ(p,a) y s = δ(q,a):

Si (r, s) ya ha sido marcado, entonces p y q también son distinguibles, por lo tanto marcar la entrada (p, q).

De lo contrario, colocar (p, q) en una lista asociada a la entrada (r, s).

Agrupar los pares de estados no marcados.

Luego del tercer paso, si la tabla creada queda completamente marcada, entonces el AFD inicial ya era mínimo.

La complejidad computacional del problema de minimizar un AFD es polinomial. De hecho, existen algoritmos más eficientes aún que el mostrado en este artículo (aunque menos intuitivos).11 Sin embargo, el problema de minimizar un autómata finito no determinista es NP-completo y PSPACE-completo.

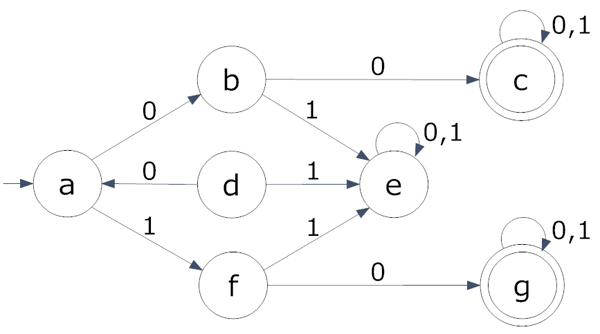
Ejemplo: En la primera figura del ejemplo, se muestra un autómata con el estado inaccesible d, el cual puede eliminarse inmediatamente. Luego se construye la tabla de pares de estados, y a continuación se marcan, de acuerdo a la tercera línea del algoritmo, las filas y columnas correspondientes a los estados finales c y g, salvo la celda que representa el par (c,g), puesto que al ser ambos estados finales, pueden ser estados equivalentes. Posteriormente, se marcan las celdas restantes de acuerdo a la cuarta línea del algoritmo, notando que el par (b, f) queda asociado con el par (c, g), y así finalmente se obtiene el autómata final, agrupando los estados b y f, así como c y g, tal y como se muestra en la segunda figura del ejemplo.

3.5 Aplicaciones (definición de un
caso de estudio)

Inicialmente el semáforo esta en rojo para el peatón y se supone que acaba de pasar a rojo. Se requiere garantizar que el semáforo permanezca en rojo al menos cuatro ticks de reloj. Esto quiere decir que si el peatón oprime el botón y el semáforo acaba de pasar a rojo debe esperar cuatro ticks de reloj para que pase a amarillo (y luego a verde); si han pasado dos ticks solo debe esperar dos ticks; y si han pasado10 cambia inmediatamente. Oprimir el botón mas de una vez no afecta el comportamiento. El semáforo permanece verde por cuatro ticks

de reloj.

Como un ejemplo de búsqueda de inteligencia y desarrollo de Vida Artificial, de hecho, no quiere decir que los Autómatas Celulares sean inteligentes, más en cambio poseen aspectos principales de la vida, y tienden a imitar procesos y comportamientos de los seres vivos. Los procesos celulares también tienen un gran vinculo de la Vida Artificial, teniendo como objetivo el fenómeno de auto reproducción, donde los trabajos con Autómatas Celulares son un ejemplo del intento de alcanzar la simulación de este fenómeno

BIBLIOGRAFÌAS

Tema 3.1:
Alfonseca, M. (2006). Compiladores e Intérpretes: Teoría y Práctica. Madrid: Pearson Educación.
Investigado por: Arilenne Hernández Plascencia
Tema 3.2:

Nicolás Kovac Neuman (2005), Teoria de automatas y lenguajes formales [Pdf. Automatas y lenguajes Nikolas Kovac Neuuman]

Investigado por: Carlos Martínez Valentin

Tema 3.3:

Analisis Lexico, Automatas Finitos, Universidad Europea de Madrid, Larireate International Universities.
Investigado por: Araceli Martinez Martinez
Tema 3.4
AHO, A. V. (2008). COMPILADORES. PRINCIPIOS, TÉCNICAS Y HERRAMIENTAS. Segunda edición. Mexico: Pearson Educación.

Investigado por: Germán David Hernández Gomez
Tema 3.5
issuu.com/lourdesbarrios/docs/revista
Investigado por: Jonathan Hernändez Antonio